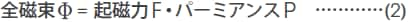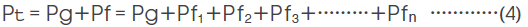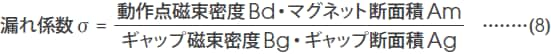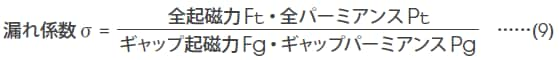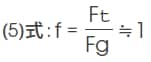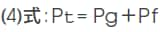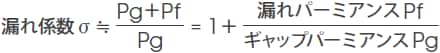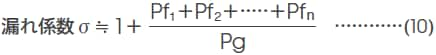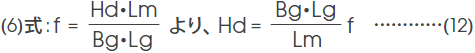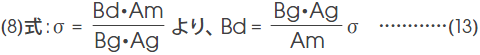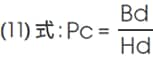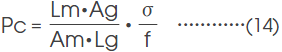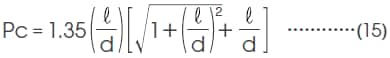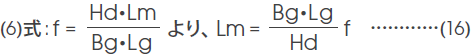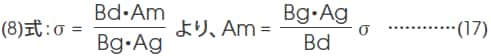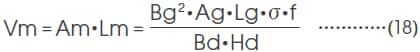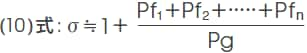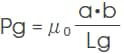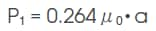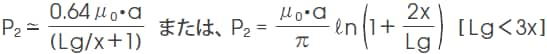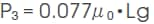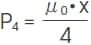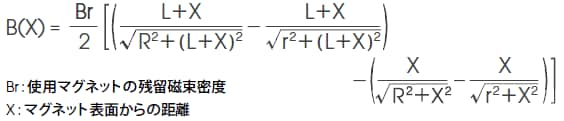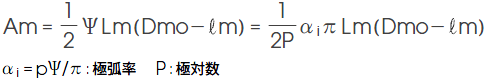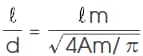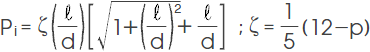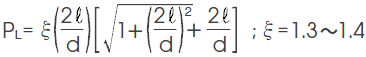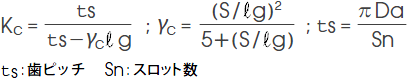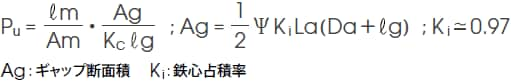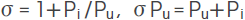マグネット

1. 基礎的な計算式

1-1. 全磁束Φとパーミアンス P

磁気回路の基礎計算式は、電気回路に関するオームの法則と同一です。つまり、全磁束をΦ、起磁力をF、磁気抵抗をRとすると、この3つの要素は、

の関係にあります。
しかし、磁気回路計算では、磁気抵抗Rはあまり用いられず、一般的には磁気抵抗Rの逆数であるパーミアンスPを用います。すなわち上記の関係式は、

で置き換えられます。
このパーミアンスPは、磁路の長さをL、磁路の断面積をA、磁路の透磁率をμとしたとき、

で表され、磁路長が短く、磁路断面積および透磁率が大きいほどパーミアンスが大、すなわち磁気抵抗が小さくなることを示します。
また、磁気回路全体のパーミアンスPtは、ギャップ部磁気抵抗の逆数として定義されるギャップパーミアンスPgと漏れ磁束による磁気抵抗の逆数として定義される漏れパーミアンスPfの和、すなわち、Pt＝Pg＋Pfで表され、さらに、漏れ磁束を個々の漏れ磁路空間ごとに把握する場合、全パーミアンスPtは、ギャップパーミアンスPgと磁路空間ごとの漏れパーミアンスPf₁＋Pf₂＋Pf₃……＋Pf_nの総和として表されます。

1-2. 起磁力損失係数 f

起磁力損失係数fは、磁気回路中の全起磁力Ftとギャップの起磁力Fgとの比、

として定義されます。
磁気回路の全起磁力Ftは、使用されるマグネットによって与えられ、その値は、マグネット動作点の磁界強度Hdとマグネットの長さLmの積となります。
また、ギャップの起磁力Fgは、ギャップの磁束密度Bgとギャップの長さLgとの積として与えられますから、(5)式は、

に展開できます。

1-3. 漏れ係数σ

漏れ係数σは、磁気回路中のマグネットから発生する全磁束Φtとギャップに収束されたギャップ磁束Φgとの比、すなわち、

で表されます。
マグネットから発生する全磁束Φtは、マグネット動作点の磁束密度Bdとマグネットの断面積Amの積で与えられ、ギャップに収束された磁束Φgはギャップの磁束密度Bgとギャップ断面積Agとの積で与えられますから、(7)式は、

に展開できます。
また、(2)式：Φ=FPにより、(7)式は、

とも表すことができ、起磁力損失係数fは、一般に1に近い値になりますので、(9)式は

となり、Pfを個々の漏れ磁路空間ごとに分割して、

という形で表すこともできます。

1-4. パーミアンス係数Pc

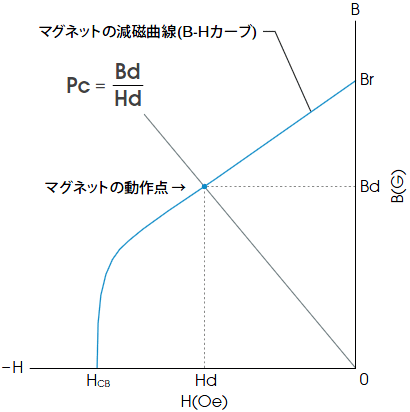
B-Hカーブ上のマグネットの動作点を表すのにパーミアンス係数Pcが用いられます。この値は、動作点の磁束密度Bdと磁界強度Hdの比として定義され、

で表されます(下図参照)。

1-4-a. 磁気回路に組み込まれたマグネットのパーミアンス係数

磁気回路に組み込まれたマグネットのパーミアンス係数は、(6)式および(8)式からHd、Bdを求め、それを(11)式に代入することで得ることができます。

が得られます。

1-4-b. マグネット単体のパーミアンス係数

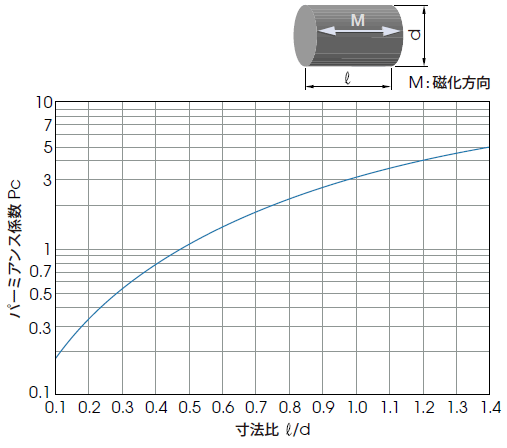
マグネットが単体で存在する場合のパーミアンス係数は、マグネットの形状に大きく左右され、正確な値を計算で求めることは非常に困難です。
そこで、円柱状のマグネットを試料とした下図(寸法比とパーミアンス係数の関係グラフ)から、おおよその目安を得ます。

近似式としては、

となります。

1-5. 長さLm、断面積Am、体積Vmの計算法

マグネットに必要となる長さLm、断面積Amは

となり、この式から、Hd、Bd、Bg、Ag、Lgおよびf とσを与えることにより、必要なLm、Amを求めることができます。
また、必要な体積Vmは、

となり、必要なマグネットの体積は、その動作点のエネルギー積に逆比例することがわかります。

1-6. 漏れ係数σ、起磁力損失係数fを求める方法

1-6-a. 実験的にσ、fを求める場合の手順

■ サーチコイルを用いる方法

1. 1. マグネットにサーチコイルを巻いてギャップ磁束を測定する。
2. 2. トータルフラックスΦg/マグネット断面積AmからBdを算出する。
3. 3. B-Hカーブ(減磁曲線)からHdを求める。
4. 4. Bg、Ag、Lg、Am、Lmを実測する。
5. 5. (6)式、(8)式よりf、σを算出する。

■ サーチコイルを用いない方法

1. 1. f値を仮定する(一般的には1.0～1.2)。
2. 2. Lm、Bg、Lgを実測する。
3. 3. 前頁の(12)式によりHdを算出する。
4. 4. B-Hカーブ(減磁曲線)からBdを求める。
5. 5. Am、Agを実測し、(8)式よりσを算出する。

1-6-b. 計算によりσを求める方法

PgとPf₁～Pf_nを計算で求めてσを算出します。

参考例

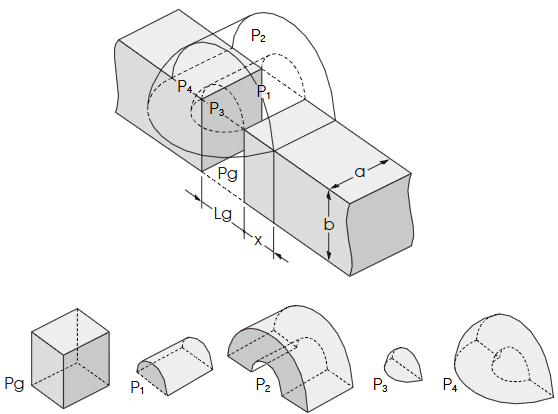
漏れ磁路空間・基本構成パーツ(Pg、P₁、P₂、P₃、P₄)のパーミアンス計算例を以下に示します。

1） 空隙部分(図中のギャップ空間部分)のパーミアンス

2） 半円柱漏れ磁路のパーミアンス

3） 中空状半円柱漏れ磁路のパーミアンス

4） 4分球漏れ磁路のパーミアンス

5） 中空状4分球(4分球殻)漏れ磁路のパーミアンス

上記1)～ 5) のパーミアンスを組み合わせることによって、漏れ磁路空間における概略のσを求めることができます(μ₀：真空の透磁率)。

2. マグネット中心線上の磁束密度B(X)計算式

B-Hカーブが直線か、または屈曲点より上に動作点Bdがある場合、マグネットの外部における磁界分布の様子は、マグネットと等しい透磁率を持つ同一断面形状、長さXの空間を想定し、その外周面における閉路電流から発生する磁界と同様に考えることができます。
以下、代表的な3つの形状について、このB(X)を求める計算式を示します。これらの式は、フェライトマグネットおよびネオジムマグネットにおいて近似式として有効です。

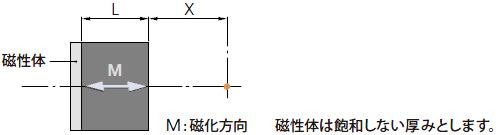
2-1. 円柱状マグネット

　

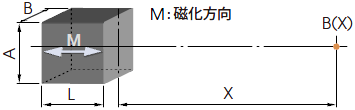
2-2. 角柱状マグネット

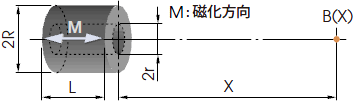
2-3. 円筒状マグネット

2-4. 磁極裏面に磁性体のある場合

2-1、2-2、2-3式のL 項に2Lを代入します。

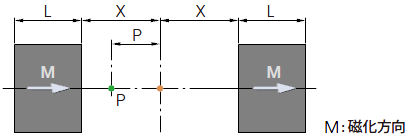
2-5. 同一形状のマグネットが2Xの距離で対向する場合

ギャップ中心でのB(X)は、2-1、2-2、2-3式で求めたB(X)の2倍になります。
また、ギャップ中のP点におけるB(X)は、前式X項にX－Pを代入したB(X－P)とX＋Pを代入したB(X＋P)の和になります。

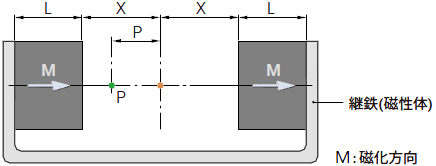
2-6. 前項と同様の配置で、磁極裏面に磁性体がある場合

2-1、2-2、2-3式のL 項に2Lを代入し、ギャップ中心およびギャップ中のP点におけるB(X)は、2-5項と同じ手順になります。

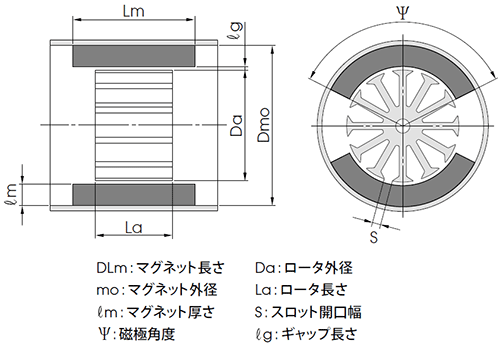
3. モータ用磁気回路の有効磁束数計算

モータ用磁気回路は、ロータのスロット数、スロット形状、ケース肉厚などの要素によって磁気回路条件が大きく異なります。したがって、この項は、考え方の基本を示す数式のみ示します。

1) マグネット断面積 Am

2） マグネット等価寸法比 ℓ/d

3） マグネット単体の漏れパーミアンス係数 Pi

4） ヨーク部含むマグネット単体のパーミアンス係数 PL

5） カーター係数 Kc

6) 有効パーミアンス係数 P_u

7) 漏れ磁束σ

8) 極の磁束(あるいは有効磁束)Φg

磁気回路の飽和について
以上のΦg算出方法は、磁気回路の飽和については考慮していません。しかし、実際の磁気回路においては、ケース、ロータ部分に飽和現象が起きることも考えられます。つまり、上記算出方法で得られたΦgと実際のモータにおけるΦgを比較した場合、実際のモータでのΦgが計算値より小さい場合は、磁気回路が飽和していることが考えられます。

SI単位/CGS単位対照換算表

SI単位系の特性値に　印左側の換算比を乗ずるとCGS系の値になります。
同様に、CGS系の特性値に　印右側の換算比を乗ずるとSI単位系の値となります。

SI単位系▶					◀CGS単位系
磁気量	量記号	単位名	単位記号	換算比▶	◀換算比	単位記号	単位名
磁束	Φ	ウェーバ	Wb	108▶	◀10-8	Mx	マウスウェル
磁束密度	B	テスラ	T	104▶	◀10-4	G	ガウス
磁界の強さ	H	アンペア/m	A/m	4π×10-3▶	◀103/4π	Oe	エルステッド
磁化の強さ	M	アンペア/m	A/m	10-3▶	◀103	G	ガウス
磁気分極	J	テスラ	T	104/4π▶	◀4π×10-4	G	ガウス
起磁力	Fm	アンペア	A	4π×10-1▶	◀10/4π	Gi	ギルバート
磁気吸引力	F	ニュートン	N	105▶	◀10-5	dyn	ダイン
透磁率	μ	ヘンリー/m	H/m	107/4π▶	◀4π×10-7	無名数
真空の透磁率	μ0	4π×10-7ヘンリー/m	H/m			無名数	1
磁気抵抗	Rm	1/ヘンリー	H-1	4π×10-9▶	◀109/4π	Gi/Mx	ギルバート/マクスウェル
パーミアンス	P	ヘンリー	H	109/4π▶	◀4π×10-9	Mx/Gi	マクスウェル/ギルバート
磁気エネルギー積	BH	ジュール/m3	J/m3	4π×10▶	◀10-1/4π	G・Oe	ガウス・エルステッド
				10▶	10-1	erg/cm3	エルグ/cm3